Unit Circle
When working with the unit circle, it’s essential to understand how angles and standard position relate to one another. The concept of standard position is simple: imagine an angle where its vertex is at the origin of the circle, and one ray lies along the positive x-axis. The second ray will be placed at the specific angle measure, moving counter-clockwise.
This idea is crucial because it helps in measuring angles, whether in degrees or radians. For example, a right angle measures 90°, while a straight angle is 180°. You can even express these angles in radians, such as π radians for 180° or 3π/2 rad for 270°. The conversion factor between radians and degrees is straightforward: π rad = 180°. This makes it easy to convert between them and understand their relationship.
The unit circle has a radius of 1, which simplifies many calculations, like finding the circumference or area. Since it’s a circle, the circumference is 2π, and the diameter is 2, which makes working with trigonometric functions simpler. When using the unit circle to calculate values like sine or cosine, we look at specific points where the rays intersect the circle. These points give us the x-coordinate (for cosine) and y-coordinate (for sine).
The unit circle also helps us understand the relation between sides and angles in a right triangle, providing a clear way to calculate the tangent and other trigonometric functions. By memorizing the values for common angles such as 30° (or π/6 rad), you can easily find the sine, cosine, and tangent values for various angles, helping to improve your understanding of trigonometry.
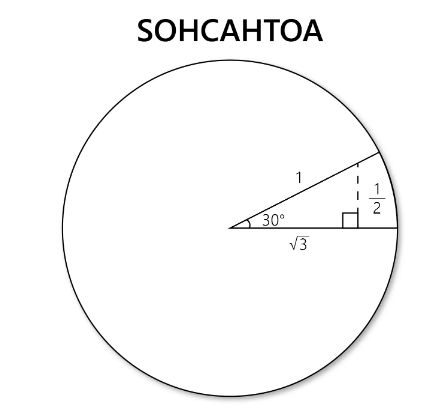
In trigonometry, understanding the unit circle is vital for finding trig values for common angles. When we work with a right triangle, we use the mnemonic SOHCAHTOA to remember how to calculate the sine, cosine, and tangent for various angles. For example, if you consider an angle of 60°, you can break it down into its opposite and adjacent sides. These sides correspond to the y-coordinate (for sine) and the x-coordinate (for cosine) of the point on the unit circle. The ray coming from the angle 60° hits the unit circle at the point (1/2, √3/2). This gives you the sine and cosine values for that angle: sin60° = √3/2 and cos60° = 1/2. For tangent, we simply divide the y-coordinate by the x-coordinate, which gives tan60° = √3.
The key to understanding all of this is placing angles in standard position. This means the vertex of the angle is at the origin of the circle, and one ray lies along the positive x-axis. The other ray is placed according to the angle measure, moving counter-clockwise from the x-axis. This standard approach makes it easy to calculate the trig values of angles using the unit circle, whether you are working with radians or degrees. By referencing these values in mathematics, you can calculate the sine, cosine, and tangent of any angle on the unit circle. Mastering this process is essential for solving trigonometric problems involving right triangles and understanding the relationships between angles and their corresponding sides.
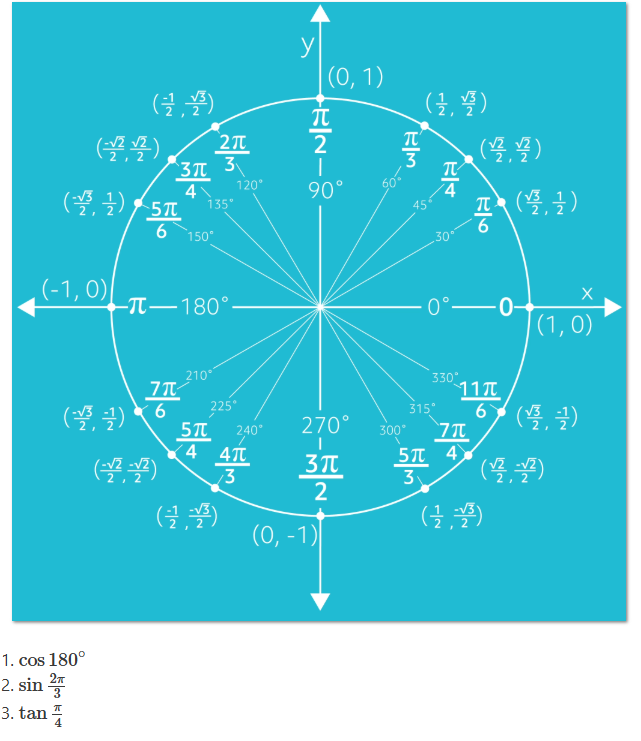
In trigonometry, the unit circle is a powerful tool for finding trig values at specific angles. For example, consider the angle 180°. The ray corresponding to this angle intersects the unit circle at the point (−1,0), so cos180° = −1. Similarly, for the angle 2π/3 rad, the point on the circle is (−1/2, √3/2), so sin2π/3 = √3/2. If we look at the angle π/4 rad, the point on the unit circle is (√2/2, √2/2), giving us tanπ/4 = 1, as 2√2/√2 = 1.
The beauty of the unit circle lies in its ability to simplify the calculation of sine, cosine, and tangent for common angles. Whether you are working in radians or degrees, you can use the conversion π rad = 180° to switch between the two. This conversion allows us to easily calculate trig values for any angle in standard position.
The standard position means the vertex of the angle is at the origin of the circle, and the ray begins along the positive x-axis, extending counter-clockwise for positive angles. Knowing these common angle measurements and their corresponding trig values is crucial for mastering trigonometric concepts in mathematics.